Creating a Solver for LinkedIn's Tango Puzzle Game

Lately, I’ve developed a small morning ritual: I open LinkedIn and tackle a quick round of Tango. What started as a casual way to wake up my brain has turned into a full-on obsession — and, over time, I’ve gotten surprisingly good at it. The puzzle’s clean design hides a deep layer of logic that rewards pattern recognition, discipline, and just the right amount of stubbornness.

As a developer, that daily habit eventually sparked a bigger question: what exactly makes these puzzles solvable every time? That curiosity led me to break Tango down into repeatable steps — and ultimately, to code a binary puzzle solver that follows the same logic I use each morning. In this post, I’ll walk through those steps and show how human reasoning can be translated into code.

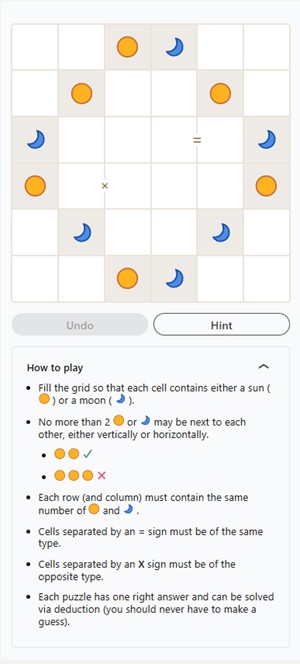
What is a binary puzzle?

Here are the rules for solving a binary puzzle:

1. Each box should contain either a zero or a one.
2. More than two equal numbers immediately next to or below each are not allowed.
3. Each row and each column should contain an equal number of zeros and ones.
4. Each row is unique and each column is unique. So, any row cannot be exactly equal to another row, and any column cannot be exactly equal to another column.

Each binary puzzle has a unique solution. It is always possible to make a next step by reasoning. In other words, the solution can always be found without guessing.

Tips on how to solve a binary puzzle

Step 1: Find pairs

Because at most two equal numbers immediately next to or below each other are allowed, pairs can be supplemented with the other number. So, in the example below, both blue boxes should contain a zero.

Step 2: Avoid trios

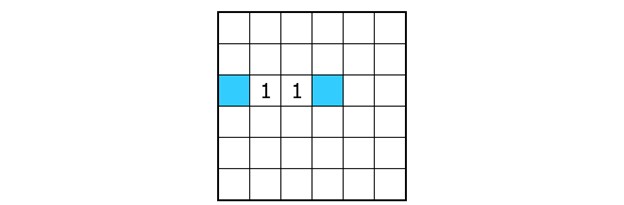
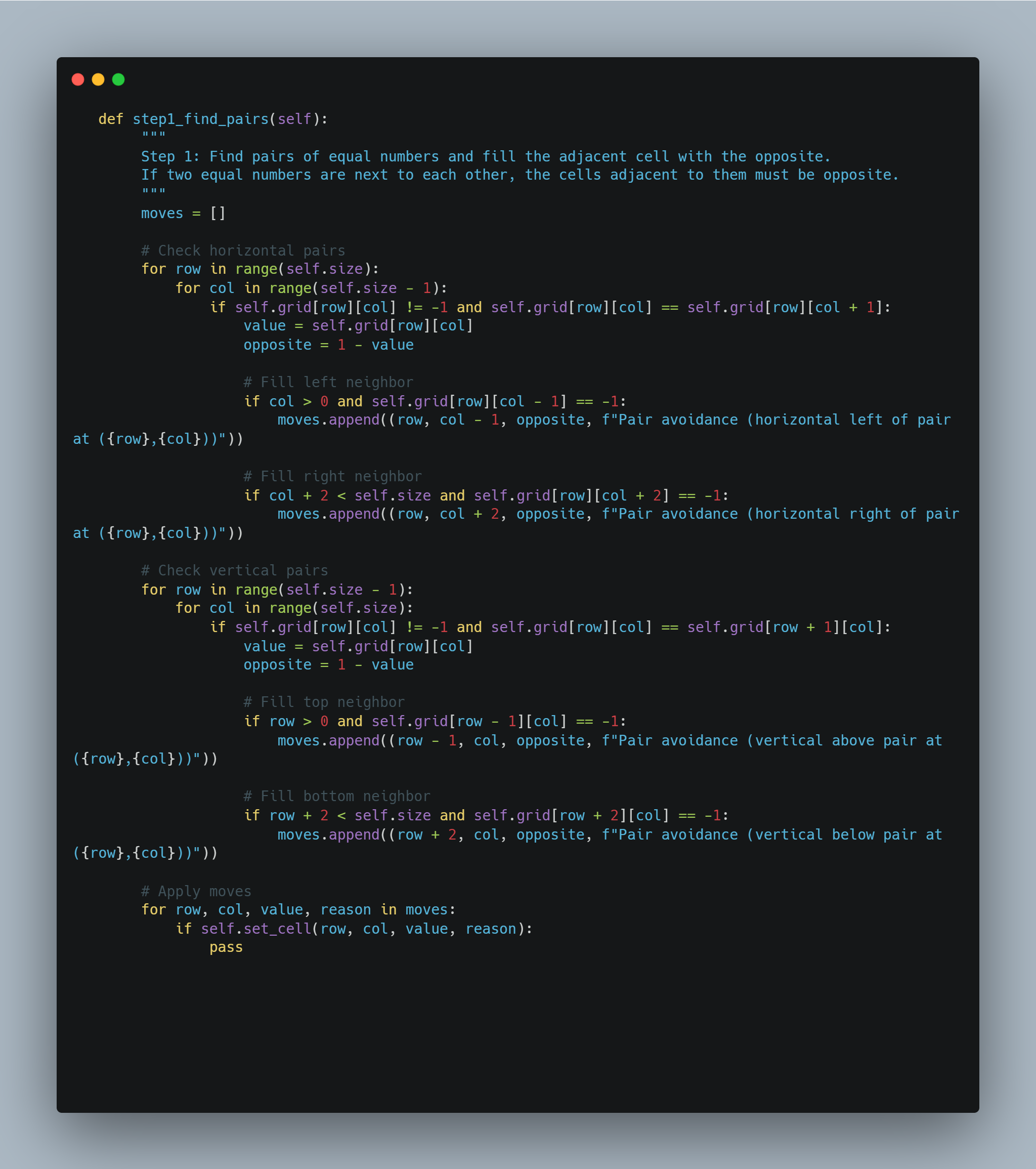
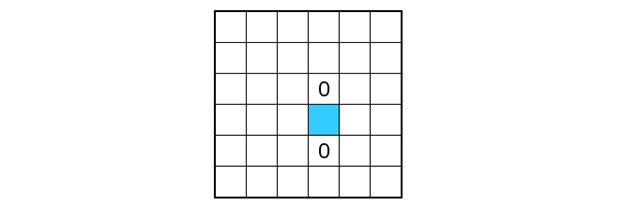
If two cells contain the same number with an empty cell in between, this empty cell should contain the other number. The blue cell in the example below should contain a one, because otherwise a trio appears.

Step 3: Complete rows and columns

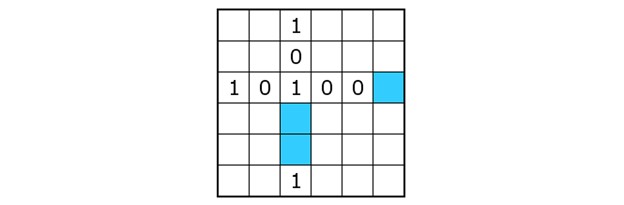
Each row and column should contain an equal number of zeros and ones. If the required number of zeros is reached in a row or a column, the remaining cells should contain one, and vice versa. In the example below, each row and column should contain 3 ones and 3 zeros. This implies that the blue cell in the third row should be a one, and that the blue cells in the third column should be zeros.

Step 4: Eliminate impossible combinations based on completed rows and columns

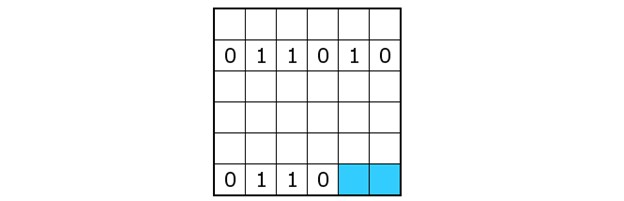
In the example below, there are one and a zero missing in the bottom row. If the one is filled in in the left blue cell and the zero in the right blue cell, the bottom row becomes equal to the second row. Because this is not allowed, the left blue cell should be a zero, and the right blue cell should be one.

Building this solver wasn’t about removing the fun from the puzzle, but about understanding it more deeply. By breaking the game down into deterministic steps, I gained a greater appreciation for both the human intuition behind solving it and the elegance of expressing that logic in code.